Heap Tree Structure을 이용하는 정렬
- Complete Binary Tree; 루트 부터 자식 노드가 왼쪽 자식 노드, 오른쪽 자식 노드로 차근차근 들어가는, 빽빽한 구조의 트리
- Heap: 최솟값, 최댓값을 최대한 빨리 찾아나기 위해 Binary Tree를 이용함
- 최대힙: 부모 > 자식
- 최소힙: 자식 > 부모
힙 생성 알고리즘(Heapify Algorithm)
예를 들어 부모 노드의 값보다 자식 노드의 값 중에 큰 값이 있다면, 부모 노드와 자식 중 가장 큰 자식 노드를 바꾸는 것 > 이렇게 하위로 갈 수록 규칙이 깨지지 않는지 쭉 탐색하면서 정렬해줘야 함
* 시간 복잡도: O(lg N) = height of Tree
* 전체 힙 생성 시간 복잡도: O(1/2N lg N) = O(N lgN) => O(N)
배열 이용 (삽입 되는 순서대로 인덱스를 붙이기)
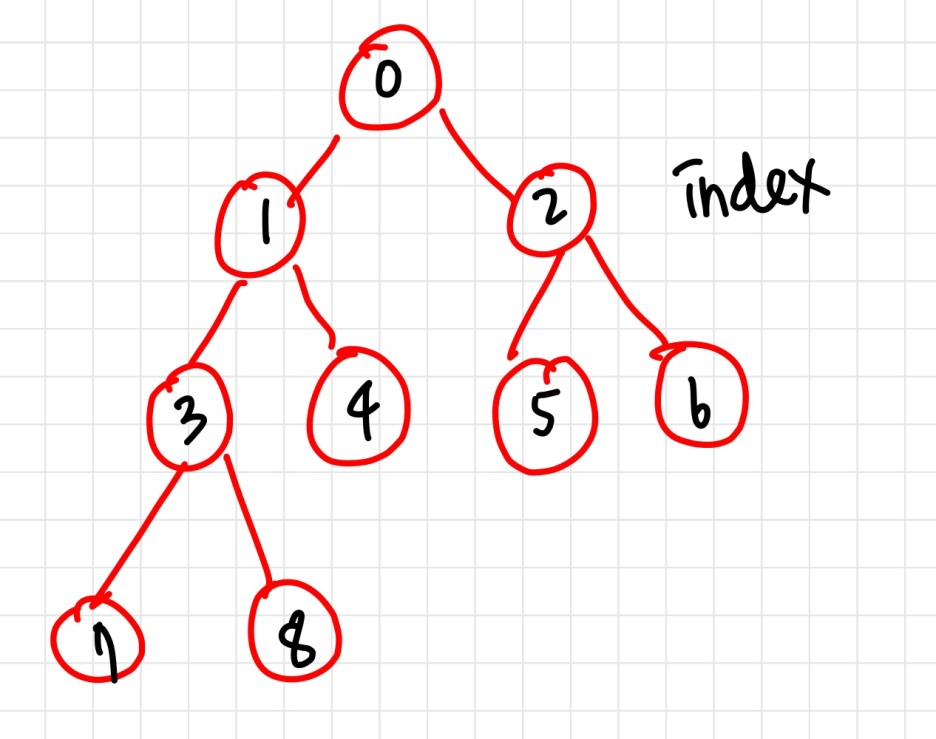
여기서 index 0, 1, 2, 3 트리만 heapify 를 수행해주면 됨
방향은 상향식, 하향식 모두 가능함. 이건 하고 싶은대로 결정하면 됨.
#include <stdio.h>
int num = 9;
int heap[9] = {7, 6, 5, 8, 3, 4, 9, 1, 6};
int main(void){
// first change tree structure into heap
for(int i = 1; i<num; i++){
int c = i;
do{
int root = (c-1)/2;
if(heap[root]<heap[c]){
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c=root;
}while(c!=0);
}
// 크기를 줄여가며 반복적으로 힙을 구성 = 순서대로 정렬되도록
for(int i = num-1; i>=0; i--){
int temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
int root = 0;
int c = 1;
do{
c=2*root+1;
// 자식 중 더 큰 값 찾기
if(heap[c]<heap[c+1] && c<i-1) { // 더 크면
c++; //더 큰 애 선택
}
// 루트보다 자식이 더 크면 교환
if(heap[root]<heap[c]&&c<i){
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c; // 자식을 루트로 해서 아래도 해봄
}while(c<i); //이미 한 번 root랑 바꾼 애들은 재정렬에서 제외함
}
for(int i = 0; i<num; i++){
printf("%d ", heap[i]);
}
}힙 정렬을 하는 부분에서 헷갈려서 안에 printheap()이라는 함수를 넣어서 루프마다 프린트를 해보았다.
#include <stdio.h>
void printheap(int* heap, int num){
for(int i = 0; i<num; i++){
printf("%d ", heap[i]);
}
}
int num = 9;
int heap[9] = {7, 6, 5, 8, 3, 4, 9, 1, 6};
int main(void){
// first change tree structure into heap
for(int i = 1; i<num; i++){
int c = i;
do{
int root = (c-1)/2;
if(heap[root]<heap[c]){
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c=root;
}while(c!=0);
}
for(int i = 0; i<num; i++){
printf("%d ", heap[i]);
}
printf("\n");
// 크기를 줄여가며 반복적으로 힙을 구성
for(int i = num-1; i>=0; i--){
int temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
printf("loop1: ");
printheap(heap, num);
printf("\n");
int root = 0;
int c = 1;
do{
c=2*root+1;
// 자식 중 더 큰 값 찾기
if(heap[c]<heap[c+1] && c<i-1) {
c++;
} // 더 큰 값 찾음
// 루트보다 자식이 더 크면 교환
if(heap[root]<heap[c]&&c<i){
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
printf("loop2(%d): ", c);
printheap(heap, num);
printf("\n");
}while(c<i); //이미 한 번 root랑 바꾼 애들은 재정렬에서 제외함
}
}
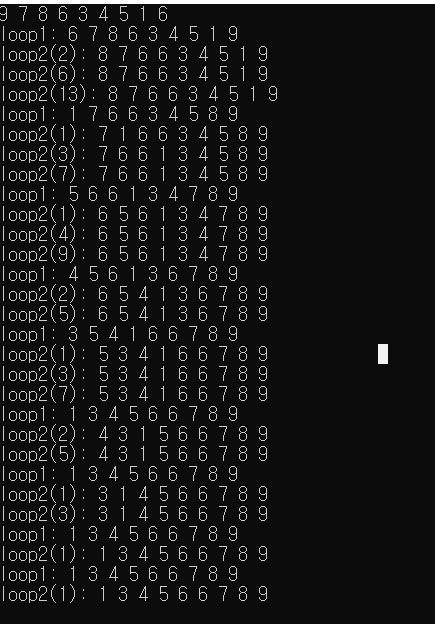
힙 구조로 변형한 후에, 작은 수부터 정렬할 때 root노드와 i번째 노드랑 위치를 바꾸고 새로 root가 된 노드의 위치를 탐색하며 아래로 내려가는데, 이때 내려가는 과정이 i단계 이전까지 라는 것을 간과해서 처음에 이해가 안됐다...
'컴퓨터기본 > 알고리즘' 카테고리의 다른 글
| 6. 스택 (Stack), 큐 (Queue) (0) | 2021.06.14 |
|---|---|
| 5. 계수 정렬 (Counting Sort) (0) | 2021.06.14 |
| 3. 퀵 정렬 (Quick Sort), 병합 정렬 (Merge Sort) (0) | 2021.06.14 |
| 2. O(n²) 알고리즘(선택, 버블, 삽입 정렬) (0) | 2021.06.14 |
| 1. Greedy 알고리즘 (탐욕법) (0) | 2021.06.14 |